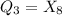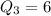Question

Using the data: 2, 2, 3, 3, 3, 4, 5, 6, 6, 19

What is Q1 and Q3

Answer 1

Q1: 2.5

Q3: 6

Explanation:

The median area is 3 and 4.

The lower quartile is 3+2=5 5/2 2.5

The upper quartile is 6+6= 12 12/2 6

Answer 2

`Q_1=2`

`Q_3=6`

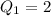
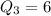
Explanation:

Notice that we already have the data sorted from least to greatest.

Now to find Q1 and Q3 we can use the following formulas

For a set of data ordered from least to greatest of the form
`X_1, X_2, ..., X_n`

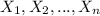
Where n is the total number of data

`Q_1=X_{(1)/(4)(n+1)}`

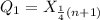
In this case
`n=10`

So:

`Q_1=X_{(1)/(4)(10+1)}`

`Q_1=X_(2.75)`

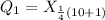
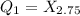
Round the nearest whole and get:

`Q_1=X_(3)`

`Q_1=3`

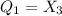
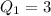
For Q3 we have:

`Q_3=X_{(3)/(4)(n+1)}`

`Q_3=X_{(3)/(4)(10+1)}`

`Q_3=X_(8.25)`

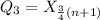
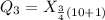
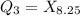
Round the nearest whole and get:

`Q_3=X_(8)`

`Q_3=6`