Answer:
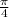

Explanation:
The answer uses the unit circle and that sine and cosecant are reciprocals.
The first choice doesn't even fit the criteria that
 is between
is between
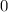 and
and
 (inclusive of both endpoints) because of the
(inclusive of both endpoints) because of the
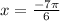 .
.
Let's check the second choice.
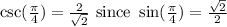 .
.
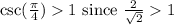
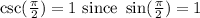 which means
which means
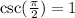 which is not greater than 1.
which is not greater than 1.
So we can eliminate second choice.
Let's look at the third.
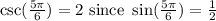 which means
which means
 .
.
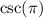 isn't defined because
isn't defined because
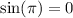 .
.
So we are eliminating 3rd choice now.
Let's look at the fourth choice.
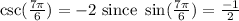 which means
which means
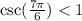 and not greater than 1.
and not greater than 1.
I was looking at the rows as if they were choices.
Let me break up my choices.
So we said
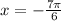 doesn't work because it is not included in the inequality
doesn't work because it is not included in the inequality
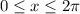 .
.
How about
 ? This leads to
? This leads to
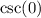 which doesn't exist because
which doesn't exist because
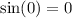 .
.
So neither of the first two choices on the first row.
Let's look at the second row again.
We said
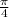 worked but not
worked but not

Let's look at the choices on the third row.
We said
 worked but not
worked but not

Let's look at at the last choice.
We said it gave something less than 1 so this choice doesn't work.