Answer:
Geometric Sequence.

Explanation:
The x-coordinates represent the number of terms of the sequence while the y-coordinates represent the term of the sequence. So the series shown on the graph is:
1, 2, 4, 8
We can see that the ratio of two consecutive terms of the above sequence is constant. i.e.
2/1 = 2
4/2 = 2
8/4 = 2
Such a sequence in which the ratio of two consecutive terms is a constant is known as Geometric Sequence and this constant ratio is known as common ratio.
The general term of a geometric sequence is represented as:
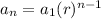
Using the values for the given sequence we get:
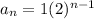

Where n represents the number of term.