Question

The number of lattes sold daily for two coffee shops is shown in the table:

Lattes
55
52
50
47
68
48
53
53


Based on the data, what is the difference between the median of the data, including the possible outlier and excluding the possible outlier?

Answer 1

0.5

Explanation:

i finished the assignment and it was right so yeah it’s 0.5

Answer 2

0.5

Explanation:

Sort the given data in ascending order:

47, 48, 50, 52, 53, 53, 55, 68

Possible outlier is number 68. Check whether this number is an outlier:

`Q_1=49\\ \\Q_2=52.5 \\ \\Q_3=54`

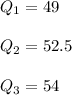
The interquartile range is

`Q_3-Q_1=54-49=5`

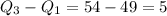
Multiply it by 1.5:

`1.5\cdot 5=7.5`

and add to third quartile:

`7.5+54=61.5`

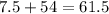
Since
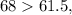`68>61.5,` number 68 is an outlier.

The median of the sample with outlier is
`Q_2=(52+53)/(2)=52.5`

The median of the sample without outlier is 52

The difference between the median of the data, including the possible outlier and excluding the possible outlier is 52.5-52=0.5