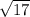Answer:
5
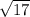 is the answer.
is the answer.
Explanation:
y= 4x-1
taking derivative with respect to x ,we get
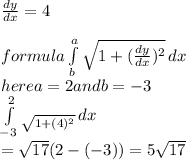
Using distance formula
we have points
at x =-3 the value of y = 4(-3)-1= -12-1 = -13
at x =2 the value of y = 4(2)-1 =7
points are ( -3,-13) and (2,7)
distance formula =
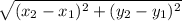
=
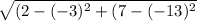
=
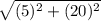
=
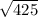
=5