Question

Life tests on a helicopter rotor bearing give a population mean value of 2500 hours and a population standard deviation of 135 hours. IThe population is normally distributed. If the specification requires that the bearing lasts at least 2100 hours, what percent of the parts are expected to fail before the 2100 hours?. List your answer as a percentage to 2 decimal places without the % sign (X.XX)

Answer 1

The percent of the parts are expected to fail before the 2100 hours is 0.15.

Explanation:

Given :Life tests on a helicopter rotor bearing give a population mean value of 2500 hours and a population standard deviation of 135 hours.

To Find : If the specification requires that the bearing lasts at least 2100 hours, what percent of the parts are expected to fail before the 2100 hours?.

Solution:

We will use z score formula

`z=(x-\mu)/(\sigma)`

Mean value =
`\mu = 2500`

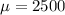
Standard deviation =
`\sigma = 135`

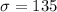
We are supposed to find If the specification requires that the bearing lasts at least 2100 hours, what percent of the parts are expected to fail before the 2100 hours?

So we are supposed to find P(z<2100)

so, x = 2100

Substitute the values in the formula

`z=(2100-2500)/(135)`

`z=−2.96`

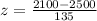
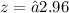
Now to find P(z<2100) we will use z table

At z = −2.96 the value is 0.0015

So, In percent =
`.0015 * 100=0.15\%`

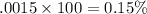
Hence The percent of the parts are expected to fail before the 2100 hours is 0.15.