Question

10 men and 12 women will be seated in a row of 22 chairs. What is the probability that all men will be seated side by side in 10 consecutive positions? 1/C(22, 10) 10!/C(22, 10) 10!/22! 10! middot 12!/22! 10! middot 13!/22!

Answer 1

The correct option is 4.

Explanation:

It is given that 10 men and 12 women will be seated in a row of 22 chairs.

Total possible ways to arrange n terms is n!.

Similarly,

Total possible ways to place 22 people on 22 chairs = 22!

`\text{Total outcomes}=22!`

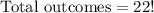
It is given that all men will be seated side by side in 10 consecutive positions.

Total possible ways to place 10 people on 10 chairs = 10!

Let 10 men = 1 unit because all men will be seated side by side in 10 consecutive positions. 12 women = 12 units because women can any where.

Total number of units = 12 + 1 = 13.

Total possible ways to place 13 units = 13!

Total possible ways to place 10 men and 12 women, when all men will be seated side by side in 10 consecutive positions is

`\text{Favorable outcomes}=10!\cdot 13!`

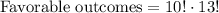
The probability that all men will be seated side by side in 10 consecutive positions

`P=\frac{\text{Favorable outcomes}}{\text{Total outcomes}}=(10!\cdot 13!)/(22!)`

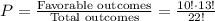
Therefore the correct option is 4.