Question

300. mL of a 3.0 M aqueous solution of Iron (III) Chloride is mixed with 353 grams of a 33.3 mass % solution of Silver (U) Nitrate and water. 267 grams of a solid precipitate forms. What is the percent yield of the reaction assuming that the solubility of the solid precipitate in water is negligible.

Answer 1

Answer: 26.9%

Explanation: The balanced equation for the reaction of Iron(III)chloride with silver nitrate is:

`FeCl_3(aq)+3AgNO_3(aq)\rightarrow Fe(NO_3)_3(aq)+3AgCl(s)`

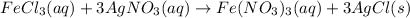
From given information, 300.0 mL of 3.0 M aqueous solution of Iron(III)chloride is mixed with 353 grams of 33.3% by mass solution of silver nitrate and water.

From this given information we will calculate the moles of each reactant.

mL of Iron(III)chloride are converted to L and then multiplied by molarity to get its moles.

`300.0mL((1L)/(1000mL))((3.0mol)/(1L))`

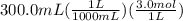
= 0.9 moles of Iron(III)chloride

33.3% by mass solution of silver nitrate means 33.3 grams of it are present in 100 grams of solution. We can calculate the grams of silver nitrate present in 353 grams of solution.

`353gSolution((33.3gAgNO_3)/(100gSolution))`

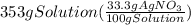
= 117.549 g of silver nitrate

Molar mass of silver nitrate is 169.87 gram per mol. Let's divide the grams by molar mass to calculate its moles.

`117.549g((1mol)/(169.87g))`

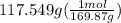
= 0.692 moles of silver nitrate

From balanced equation, Iron(III)chloride and silver nitrate react in 1:3 mol ratio. Moles of silver nitrate are less than moles of Iron(III)chloride which clearly indicates that silver nitrate is limiting reactant.

Since, there is 3:3 that is 1:1 mol ratio between silver nitrate and silver chloride, 0.692 moles of silver chloride(precipitate) will form.

Molar mass of AgCl is 143.32 gram per mol. Multiply the moles by molar mass to calculate the grams of AgCl formed.

`0.692molAgCl((143.32g)/(1mol))`

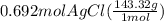
= 99.2 grams

From calculations, theoretical yield is 99.2 grams. The actual yield is given as 267 grams which is not looking good. Actual yield is always less than theoretical yield. It would be making more sense if the actual yield is 26.7 grams. So, if we do the calculations by taking the actual yield as 26.7 grams then the percent yield is calculated as:

percent yield =
`((26.7)/(99.2))*100`

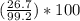
= 26.9%

So, the percent yield of the reaction will be 26.9%.