Question

6. A study was conducted to determine if there was a linear relationship between a person's age and his/her peak heart rate. Age Peak Heart Rate 16 220 26 194 32 193 37 178 42 172 53 160 48 174 21 214 A. Does the heart rate depend on the age, or does the age depend on the heart rate?

Answer 1

Let x represents the person's age and y represents the peak heart rate of the person,

Thus, the table that shows the given situation would be,

x 16 26 32 37 42 53 48 21

y 220 194 193 178 172 160 174 214,

By the above table,

`\sum x=275`

`\sum y=548`

`\sum x^2=10643`

`\sum xy=49876`

`\sum y^2=286225`

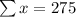
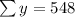
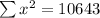
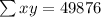
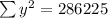
So, the correlation coefficient is,

`r=(n\sum xy-\sum x\sum y)/(√((n\sum x^2-(\sum x)^2)(n\sum y^2-(\sum y)^2)))`

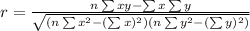
By substituting the values,

r ≈ 0.9681

Hence, there is a linear relation between x and y,

Now, let the linear equation that shows the given table,

y = b + ax

Where,

`a=((\sum y)(\sum x^2)-(\sum x)(\sum xy))/(n\sum x^2-(\sum x)^2)`

`b=(\sum xy-(\sum x)(\sum xy))/(n\sum x^2-(\sum x)^2)`

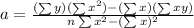
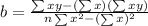
By substituting the value,

We get,

a = 241.8,

b = -1.562,

Hence, the linear equation that shows the given situation,

y = -1.562x + 241.8

Since, different values of y is obtained by substituting different values of x in the equation,

Therefore, heart rate depend on the age.