Question

(5). (10 points) There are 5 hotels in Stony Brook. If 3 people check into hotels on September 12, what is the probability that they each check into a different hotel? (What assumptions are you making?) Make sure to define any notation you use to describe elements of the sample space.

Answer 1

0.48

Explanation:

Probability that the first person chooses a hotel

⁵C₁

`^5C_1=(5!)/((5-1)!1!)\\=(120)/(24)=5`

Probability that the second person chooses a different hotel

⁴C₁

`^4C_1=(4!)/((4-1)!1!)\\=(24)/(6)=4`

because the choice of hotels has reduced by 1 as one hotel is occupied by the first person

Probability that the second person chooses a different hotel

³C₁

`^3C_1=(3!)/((3-1)!1!)\\=(6)/(2)=3`

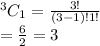
because the choice of hotels has reduced by 2 as two different hotels are occupied by the first person and second person

∴ The favorable outcomes are =⁵C₁×⁴C₁׳C₁=5×4×3=60

The total number of outcomes=5³=125

∴Probability that they each check into a different hotel=60/125=0.48