Question

uestion 2 The points A(-2, 3,-1), B(0, 5, 2) and C(-1, -2, 1) lies on the same plane. (a) Find the vector equation of the plane. (b) Find the Cartesian of the plane

Answer 1

Answer with explanation:

Equation of Plane having Direction cosines A, B and C passing through points, p, q and r is

⇒A (x-p)+B(y-q)+C(z-r)=0

The plane passes through the points A(-2, 3,-1), B(0, 5, 2) and C(-1, -2, 1).

→A(x+2)+B(y-3)+C(z+1)=0----------(1)

→A(0+2)+B(5-3)+C(2+1)=0

2 A +2 B+3 C=0

→A(-1+2)+B(-2-3)+C(1+1)=0

A -5 B+2 C=0

`\Rightarrow (A)/(4+15)=(B)/(3-4)=(C)/(-10-2)\\\\\Rightarrow (A)/(19)=(B)/(-1)=(C)/(-12)=k\\\\A=19 K,B=-K, C=-12K`

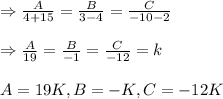
Substituting the value of A , B and C in equation (1)

⇒19 K(x+2)-K(y-3)-12 K(z+1)=0

⇒19 x +38 -y +3-12 z-12=0

⇒19 x -y -12 z +29=0, is the required equation of Plane in Cartesian form.

⇒(19 i -j -12 k)(xi +y j+z k)+29=0 ,is the required vector equation of the plane.