Answer: 77.45 %
Explanation:
We assume that the measurements are normally distributed.
Given : Mean :
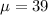
Standard deviation :
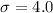
Let x be the randomly selected measurement.
Now we calculate z score for the normal distribution as :-
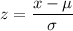
For x = 35, we have
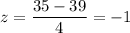
For x = 45, we have
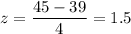
Now, the p-value =
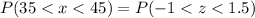
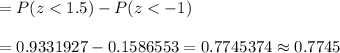
In percent ,
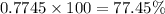
Hence, the percent of measurements should fall between 35 and 45 = 77.45 %