Question

Consider the differential equation y prime left parenthesis t right parenthesisequalst squared minus 6 y squared and the solution curve that passes through the point ​(3​,1​). What is the slope of the curve at ​(3​,1​)?

Answer 1

The slope of the curve at ​(3​,1​) is 3.

Explanation:

The given differential equation is

`y'(t)=t^2-6y^2`

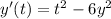
It is given that the solution curve is passing through the point ​(3​,1​).

The slope of a curve y(t) at a point (a,b) is the value of y'(t) at (a,b).

We need to find the slope of the curve at ​(3​,1​).

`m=[y'(t)]_((3,1))`

`m=[t^2-6y^2]_((3,1))`

Substitute t=3 and y=1 in the above equation, to find the slope.

`m=(3)^2-6(1)^2`

`m=9-6`

`m=3`

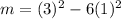
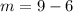
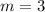
Therefore the slope of the curve at ​(3​,1​) is 3.