Question

A 2.99-m-long2.99-m-long rod, as measured in its rest frame, speeds by you longitudinally at 6.49×107 m/s6.49×107 m/s . You measure its length as it passes. By how many millimeters do you determine the rod has contracted?

Answer 1

The contraction in the rod is 71 mm.

Step-by-step explanation:

Given that,

original length L'= 2.99 m

Speed
`v= 6.49*10^(7)\ m/s`

We need to calculate the length

Using expression for length contraction

`L'=\gamma L`

`L=(L')/(\gamma)`

Where,

`\gamma=\frac{1}{\sqrt{1-(v^2)/(c^2)}}`

`L=\sqrt{1-(v^2)/(c^2)}L'`

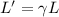
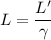
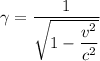
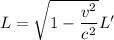
Where, v = speed of observer

c = speed of the light

Put the value into the formula

`L=\sqrt{1-((6.49*10^(7))^2)/((3*10^(8))^2)}*2.99`

`L=2.919\ m`

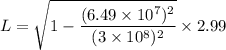
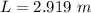
The expression for the contraction in the rod

`d =L'-L`

`d=2.99-2.919`

`d=0.071`

`d= 71\ mm`

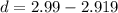
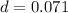
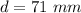
Hence, The contraction in the rod is 71 mm.