Question

74% of freshmen entering public high schools in 2006 graduated with their class in 2010. A random sample of 81 freshmen is selected. Find the probability that the proportion of students who graduated is greater than 0.743 .

Answer 1

Answer: Probability that the proportion of students who graduated is greater than 0.743 is P = 0.4755

Explanation:

Given that,

Probability of freshmen entering public high schools in 2006 graduated with their class in 2010, p = 0.74

Random sample of freshman, n = 81

Utilizing central limit theorem,

`P(\hat{p}<p) = P(Z<\hat{p} - \frac{p}{\sqrt{(p(1-p))/(n) }  } )`

So,

`(P(\hat{p}>0.743) = P(Z>0.743 - \frac{0.74}{\sqrt{(0.74(1-0.74))/(81) }  } )`

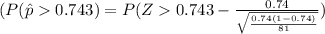
= P( Z > 0.0616)

= 0.4755 ⇒ probability that the proportion of students who graduated is greater than 0.743.