Answer: The rate of change of this quantity would be -22.50.
Explanation:
Since we have given that
the number of bottles of whiskey that a store will sell in a month at a price of p is given by
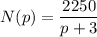
We need to find the rate of change of this quantity:
So, we will find the first derivative with respect to p.
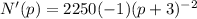
if p = 7 , then the rate of change becomes,
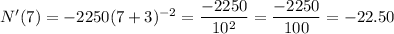
Hence, the rate of change of this quantity would be -22.50.