Question

The formula P = 0.672x^2 - 0.046x+ 3 models the approximate population P, in thousands, for a species of frogs in a particular rain forest, x years after 1999. During what year will the population reach 182 frogs? a) 2015 b) 2018 c) 2017 d) 2016 e) none

Answer 1

The correct option is d.

Explanation:

The approximate population P, in thousands, for a species of frogs in a particular rain forest, x years after 1999 is given by the formula

`P=0.672x^2-0.046x+3`

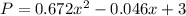
We need to find the year it which the population reach 182 frogs.

Substitute P=182 in the given formula.

`182=0.672x^2-0.046x+3`

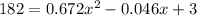
Subtract 182 from both the sides.

`0=0.672x^2-0.046x+3-182`

`0=0.672x^2-0.046x-179`

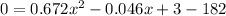
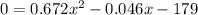
Multiply both sides by 1000 to remove decimals.

`0=672x^2-46x-179000`

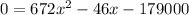
Quadratic formula:

`x=(-b\pm √(b^2-4ac))/(2a)`

Substitute a=672, b=-46 and c=-179000 in the quadratic formula.

`x=(-\left(-46\right)\pm√(\left(-46\right)^2-4\cdot \:672\left(-179000\right)))/(2\cdot \:672)`

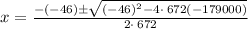
On simplification we get

`x=(-\left(-46\right)+√(\left(-46\right)^2-4\cdot \:672\left(-179000\right)))/(2\cdot \:672)\approx 16.355`

`x=(-\left(-46\right)-√(\left(-46\right)^2-4\cdot \:672\left(-179000\right)))/(2\cdot \:672)\approx -16.287`

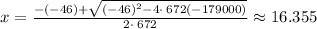
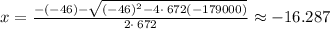
The value of x can not be negative because x is number of years after 1999.

x=16.35 in means is 17th year after 1999 the population reach 182 frogs.

`1999+17=2016`

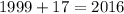
The population reach 182 frogs in 2016. Therefore the correct option is d.