Question

What is the average rate of change of the function over the interval x = 0 to x = 6?

f(x)=2x−1/3x+5
Enter your answer, as a fraction, in the box.

Answer 1

13/115

Explanation:

`f(0)=(2(0)-1)/(3(0)+5)=-(1)/(5) \\ \\ f(6)=(2(6)-1)/(3(6)+5)=(11)/(23) \\ \\ (f(6)-f(0))/(6-0) =((11)/(23)+(1)/(5))/(6)=\boxed{(13)/(115)}`

Answer 2

13/115.

Explanation:

Formula for the average rate of change of a function:

`A(x)=(f(b)-f(a))/(b-a)`

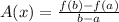
Say that b=6 and a=0.

Find the values that the function gives with these 2 values:

`f(6)=(2(6)-1)/(3(6)+5)=(11)/(23) \\\\f(0)=(2(0)-1)/(3(0)+5)=(-1)/(5) \\\\`

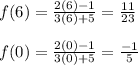
Now we substitute these values in the formula:

`A(x)=(((11)/(23) )-((-1)/(5) ))/(6-0)`

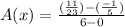
Let's solve the fraction substraction:

`(11)/(23)- (-1)/(5)=(11)/(23)+ (1)/(5)=(55)/(115)+ (23)/(115)=(78)/(115)`

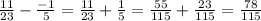
Substitute and solve the division:

`A(x)=((78)/(115) )/(6)= (78)/(115)*(1)/(6) =(78)/(690)=(13)/(115)`