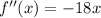Answer:
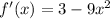 and
and
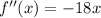
Explanation:
In order to find the derivatives, first we need to remember that for polynomial functions:
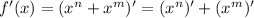 , as well as that:
, as well as that:
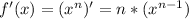
1. First derivative of the function:
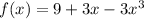
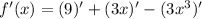 using the property
using the property
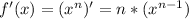 then
then
 , remember that the derivative of a constant is equal to 0
, remember that the derivative of a constant is equal to 0
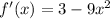
2. Second derivative:
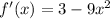
 using the property
using the property
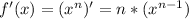 then
then
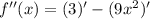
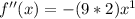
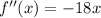
In conclusion,
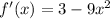 and
and