Question

If y = ½x + 1, explain why the graph will cross the y-axis at y=1​

Answer 1

see below

Explanation:

The slope intercept form of a line is

y = mx+b where m is the slope and b is the y intercept

y = 1/2x +1

The slope is 1/2 and the y intercept is 1

This means the graph crosses they y axis at 1

Answer 2

Explanation:

Ok so the slope-intercept form is represented as:
`y=mx+b`

Now in this form: m=slope, and b=y-intercept

The reason why b represents the y-intercept, is because if you look at the y-axis, any point on the y-axis has x=0, so in general a point on the y-axis can just be represented as (0, y)

So to find the y-intercept of a linear function, or in general any equation, we just plug in 0 as x.

If we do this using the general formula we get:
`y=m(0)+b`

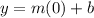
As you may know, 0 * anything = 0, so that means that we can simplify this equation to:
`y=b`. This means the y-value of the y-intercept is just going to be b, or more specifically the point is going to be at (0, b)