Let
 be the angle the dog makes with the positive horizontal. (So in the given sketch, we see the dog at an angle of
be the angle the dog makes with the positive horizontal. (So in the given sketch, we see the dog at an angle of
 , for example.)
, for example.)
When
 ranges from
ranges from
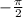 to
to
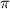 , so the angle subtended by the arc traced out by the dog in this range measures
, so the angle subtended by the arc traced out by the dog in this range measures
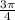 , it can cover a total area of 3/4 of a circle with radius 5 m, or
, it can cover a total area of 3/4 of a circle with radius 5 m, or
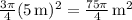 .
.
When
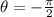 or
or
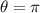 , the leash is flush against the wall, at which point the remaining free space is the sector of a circle subtended by an angle of 180 - 135 = 45 degrees, or
, the leash is flush against the wall, at which point the remaining free space is the sector of a circle subtended by an angle of 180 - 135 = 45 degrees, or
 radians, with radius 4 m. There's one sector like this on either side of the wall, so the remaining area the dog can reach is
radians, with radius 4 m. There's one sector like this on either side of the wall, so the remaining area the dog can reach is
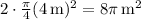 .
.
Then the total area the dog can cover is
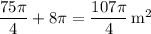
so that
 and
and
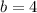 , and hence
, and hence
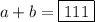 .
.