Question

\sum_{n=1}^{\infty } ((-1^n)/n)x^n

Find the interval of convergence.

Answer 1

(-1,1).

Explanation:

We need to calculate
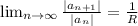`\lim_(n \to \infty)(| a_(n+1)|)/(| a_(n)|) = (1)/(R)` where R is the radius of convergence.

`\lim_(n \to \infty)((|(-1)^(n+1)|)/(|n+1|))/((|(-1)^(n)|)/(|n|))`

`\lim_(n \to \infty)((1)/(|n+1|))/((1)/(|n|))`

`\lim_(n \to \infty)(|n|)/(|n+1|)`

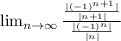
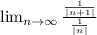
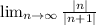
Applying LHopital rule we obtaing that the limit is 1. So
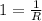`1=(1)/(R)` then R = 1.

As the serie is the form
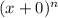`(x+0)^(n)` we center the interval in 0. So the interval is (0-1,0+1) = (-1,1). We don't include the extrem values -1 and 1 because in those values the serie diverges.