Question

Triangle ABC has vertices A(0,0) B(6,8) and C(8,4). Which equation represents the perpendicular bisected of BC?

Answer 1

`y = (1)/(2)x+(5)/(2)`

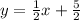
Explanation:

The perpendicular bisector of a line passes through the mid-point of the line and the product of slopes of the line and perpendicular bisector will be -1.

So,

`Mid-point\ of\ BC = ((6+8)/(2),  (8+4)/(2))\\= ((14)/(2),  (12)/(2))\\= (7,6)`

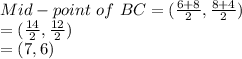
The line will pass through (7,6)

Now,

`Slope\ of\ BC = m_1 = (y_2-y_1)/(x_2-x_1) \\=(4-8)/(8-6)\\= (-4)/(2)\\= -2`

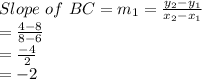
Let

m_2 be the slope of perpendicular bisector

So,

m_1*m_2 = -1

-2 * m_2 = -1

m_2 = -1/-2 = 1/2

The standard equation of line is:

y=mx+b

Where m is slope

So putting the value of slope and point to find the value of b

`6 = (1)/(2)*7 +b\\ 6 = (7)/(2) + b\\b = 6 - (7)/(2)\\ b = (12-7)/(2)\\b = (5)/(2)\\So,\ the\ equation\ of\ perpendcular\ bisector\ of\ BC\ is:\\y = (1)/(2)x+(5)/(2)`

..