Question

What is the solutions to the equation below x^2+10x+25=2
If there are more then one that’s ok

Answer 1

`x1=-5+√(2) \\x2=-5-√(2)`

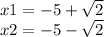
Explanation:

First we need to simplify your equation by grouping coefficients:

`x^(2) +10x+23=0`

Now, there are two valid values for your variable, wich are determined by the following expressions:

`x=\frac{-b+\sqrt{b^(2)-4ac } }{2a} \\\\x=\frac{-b-\sqrt{b^(2)-4ac } }{2a}`

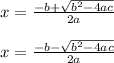
We will call those expression as (eq1) and (eq2) in their respective order

In both scenarios the following is derived from your grouped equation.

`a=1\\b=10\\c=23`

`x1=\frac{-10+\sqrt{10^(2)-4*1*23 } }{2*1}\\x2=\frac{-10-\sqrt{10^(2)-4*1*23 } }{2*1}`

`x1=(-10+√(8 ) )/(2)\\\\x2=(-10-√(8) )/(2)`

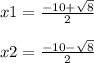
We can simplify these expressions a little more by doing the following

`x1=(-10+2 √(2 ) )/(2)\\\\x2=(-10-2√(2) )/(2)`

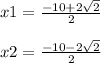
The result is

`x1=-5+√(2) \\x2=-5-√(2)`

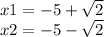
We can not simplify these expresions anymore