Answer:
Option 1 - 10.2 inches.
Explanation:
Given : The lengths of two sides of a right triangle are 12 inches and 15 inches.
To find : What is the difference between the two possible lengths of the third side of the triangle?
Solution :
Since, It is a right angle triangle so we apply Pythagoras theorem,

Where, C is the hypotenuse the longer side of the triangle
A is the perpendicular
B is the base
There will be two cases,
1) Assume that C=15 inches and B = 12 inches
Substitute the value in the formula,
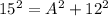
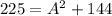
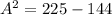
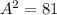
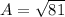
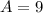
Assume that A=15 inches and B = 12 inches
Substitute the value in the formula,
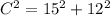

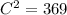
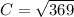
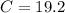
Therefore, The possible length of the third side of the triangle is
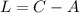
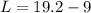
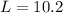
Therefore, The difference between the two possible lengths of the third side of the triangle is 10.2 inches.
So, Option 1 is correct.