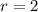Question

The equation of a circle is given below. Identify the radius and center.

x^2 + y^2 + 6x -8y +21 = 0

Answer 1

`(x-a)^2+(y-b)^2=r^2`

center -
`(a,b)`

`x^2 + y^2 + 6x -8y +21 = 0 \\x^2+6x+9+y^2-8y+16-4=0\\(x+3)^2+(y-4)^2=4`

center -
`(-3,4)`

`r=2`

Answer 2

The center is:
`(-3, 4)` and the radius is
`r=2`

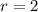
Explanation:

The general equation of a circle has the following formula:

`(x-h)^2 + (y-k)^2 = r^2\\`

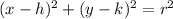
Where r is the radius of the circle and (h, k) is the center of the circle

In this case we have the following equation

`x^2 + y^2 + 6x -8y +21 = 0`

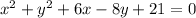
To find the radius and the center of this cicunference we must rewrite the equation in the general form of a circumference completing the Square

`(x^2 + 6x)+ (y^2 -8y) +21 = 0\\\\(x^2 + 6x+9)+ (y^2 -8y+16) +21 = 9+16\\\\(x^2 + 6x+9)+ (y^2 -8y+16) = 9+16-21\\\\(x+3)^2+ (y-4)^2 = 4\\\\(x+3)^2+ (y-4)^2 = 2^2`

Then the center is:
`(-3, 4)` and the radius is
`r=2`