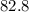Question

Given the triangle below, what is m

Answer 1

82.8 degrees

Explanation:

The information given here SSS. That means side-side-side.

So we get to use law of cosines.

`(\text{ the side opposite the angle you want to find })^2=a^2+b^2-2ab \cos(\text{ the angle you want to find})`

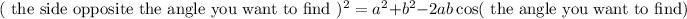
Let's enter are values in.

`12^2=10^2+8^2-2(10)(8) \cos(B)`

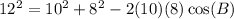
I'm going to a little simplification like multiplication and exponents.

`144=100+64-160 \cos(B)`

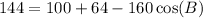
I'm going to some more simplification like addition.

`144=164-160\cos(B)`

Now time for the solving part.

I'm going to subtract 164 on both sides:

`-20=-160\cos(B)`

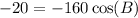
I'm going to divide both sides by -160:

`(-20)/(-160)=\cos(B)`

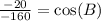
Simplifying left hand side fraction a little:

`(1)/(8)=\cos(B)`

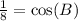
Now to find B since it is inside the cosine, we just have to do the inverse of cosine.

That looks like one of these:

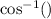`\cos^(-1)( )` or
`\arccos( )`

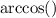
Pick your favorite notation there. They are the same.

`\cos^(-1)((1)/(8))=B`

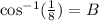
To the calculator now:

`82.81924422=B`

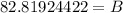
Round answer to nearest tenths:

`82.8`