Question

How much would $200 invested at 7% interest compounded annually be

worth after 5 years? Round your answer to the nearest cent.

Answer 1

$280.51

Explanation:

The formula we want to use:

`A=P(1+(r)/(n))^(nt)`

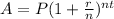
where:

P is the principal

r is the the rate

n is the number of compounding per year

t is total number of years

A is the ending amount

We are given P=200, r=.07, n=1 (compounded once a year), t=5.

So plugging this in:

`A=200(1+(.07)/(1))^(1 \cdot 5)`

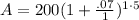
Simplify a little:

`A=200(1+.07)^(5)`

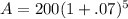
Just a little more:

`A=200(1.07)^(5)`

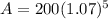
Now I'm going to put the rest of this in the calculator:

200*(1.07)^5 is what I'm putting in my calculator.

This is approximately 280.5103461.

To the nearest cent this is 280.51