Question

Ml(d^2θ/dt^2) =-mgθ

1. From the linearized equation, justify Galileo’s observation that the period of a pendulum depends only on its length and not on the mass or on the initial displacement.

Answer 1

The equation of motion of a pendulum is:

`\frac{\textrm{d}^2\theta}{\textrm{d}t^2} = -(g)/(\ell)\sin\theta,`

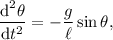
where
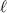`\ell` it its length and
`g` is the gravitational acceleration. Notice that the mass is absent from the equation! This is quite hard to solve, but for small angles (
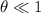`\theta \ll 1`), we can use:

`\sin\theta \simeq \theta.`

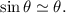
Additionally, let us define:

`\omega^2\equiv(g)/(\ell).`

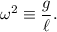
We can now write:

`\frac{\textrm{d}^2\theta}{\textrm{d}t^2} = -\omega^2\theta.`

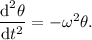
The solution to this differential equation is:

`\theta(t) = A\sin(\omega t + \phi),`

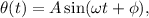
where
`A` and
`\phi` are constants to be determined using the initial conditions. Notice that they will not have any influence on the period, since it is given simply by:

`T = (2\pi)/(\omega) = 2\pi\sqrt{(g)/(\ell)}.`

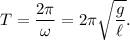
This justifies that the period depends only on the pendulum's length.