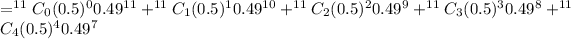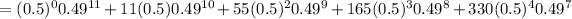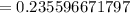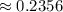Question

Assume that when adults with smartphones are randomly​ selected, 51​% use them in meetings or classes. If 11 adult smartphone users are randomly​ selected, find the probability that fewer than 5 of them use their smartphones in meetings or classes.

Answer 1

The probability is 0.2356.

Explanation:

Let X is the event of using the smartphone in meetings or classes,

Given,

The probability of using the smartphone in meetings or classes, p = 51 % = 0.51,

So, the probability of not using smartphone in meetings or classes, q = 1 - p = 1 - 0.51 = 0.49,

Thus, the probability that fewer than 5 of them use their smartphones in meetings or classes.

P(X<5) = P(X=0) + P(X=1) + P(X=2) + P(X=3)+P(X=4)

Since, binomial distribution formula is,

`P(x) = ^nC_r p^x q^(n-x)`

Where,
`^nC_r=(n!)/(r!(n-r)!)`

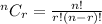
Here, n = 11,

Hence, the probability that fewer than 5 of them use their smartphones in meetings or classes

`=^(11)C_0 (0.5)^0 0.49^(11)+^(11)C_1 (0.5)^1 0.49^(10)+^(11)C_2 (0.5)^2 0.49^(9)+^(11)C_3 (0.5)^3 0.49^(8)+^(11)C_4 (0.5)^4 0.49^(7)`

`=(0.5)^0 0.49^(11)+11(0.5)0.49^(10) + 55(0.5)^2 0.49^(9)+165 (0.5)^3 0.49^(8) +330(0.5)^4 0.49^(7)`

`=0.235596671797`

`\approx 0.2356`