Question

Assume that on a standardized test of 100 questions, a person has a probability of 80% of answering any particular question correctly. Find the probability of answering between 74 and 84 questions

Answer 1

Answer: 0.7264

Explanation:

The number of independent questions (n) = 100

Probability of answering a question (p) = 0.80

Let X be the no. of questions that need to be answered.

`\therefore` random variable X follows binomial distribution

The probability function of a binomial distribution is given as

`P(X=x) = \binom{n}{x}* p^(x)(1-p)^(n-x)`

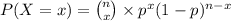
Now , we nee to find P(74 ≤ X ≤ 84)

`\therefore P(74\leq X\leq 84) = P(X=74) + P(X=75).........+ P(X=84)`

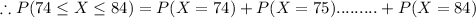
P(74 ≤ X ≤ 84) =
`\sum_(74)^(84)\binom{100}{x}* (0.80)^(x)(0.20)^(100-x)`

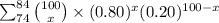
P(74 ≤ X ≤ 84) = 0.7264