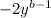Answer:
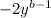
Explanation:

In multiplication of fractions you can do this:
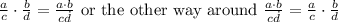 .
.
So that is exactly what we are going to do here:


We know that 12 divided by -6=12/-6 =-2.
We also know assuming x isn't 0 that x^a/x^a=1.
On the last fraction, the only thing you can do there to simplify is use the following law of exponents:
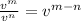 .
.
So we have


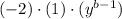
Simplifying a bit and leaving out the ( ).