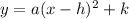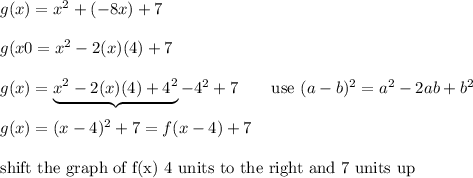Answer:
Shift the graph of f(x) 4 units to the right
and 7 units up
Explanation:
f(x) + n - shift a graph of f(x) n units up
f(x) - n - shift a graph of f(x) n units down
f(x + n) - shift a graph of f(x) n units to the left
f(x - n) - shift a graph of f(x) n units to the right
=============================================
We have
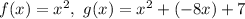
Convert the equation of g(x) to the vertex formula: