Question

Six distinct integers are picked from the set {1, 2, 3,…, 10}. How many selections are there, in which the second smallest integer in the group is 3?

Answer 1

1680 ways

Explanation:

Total number of integers = 10

Number of integers to be selected = 6

Second smallest integer must be 3. This means the smallest integer can be either 1 or 2. So, there are 2 ways to select the smallest integer and only 1 way to select the second smallest integer.

2 ways 1 way

Each of the line represent the digit in the integer.

After selecting the two digits, we have 4 places which can be filled by 7 integers. Number of ways to select 4 digits from 7 will be 7P4 = 840

Therefore, the total number of ways to form 6 distinct integers according to the given criteria will be = 1 x 2 x 840 = 1680 ways

Therefore, there are 1680 ways to pick six distinct integers.

Answer 2

70 total selections

Explanation:

The set: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10

You know that that 3 is definitly a part of the set, so you can ignore it. If 3 is the second smallest, the smallest number in the set is either 1 or 2, not both.

The number of ways to choose between 1 and 2 is
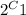`2^(C)1` ways which is equal to 2, so all that's left is choosing from the group of the set between 4 and 10.

Since you've already chosen 2 numbers (3 and 1 or 2) you need to find out how many ways can you choose 4 out of the numbers between 4 and 10. Since there are 7 numbers from 4 to 10, you need to figure out
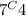`7^(C)4` which is equal to 35.

Since you are looking to find the cross between the 2, multiply 2 by 35 = 70, the answer.