Question

Solve the system of linear equations by graphing.

y = –x – 7

x + 2y = 4

What is the solution to the system of linear equations?

(–4.5, 4.25)
(–1.7, –2.8)
(0, –7)
(3, 0.5)

Answer 1

For this case we have the following system of equations:

`y = -x-7\\x+2y = 4`

Substituting the first equation in the second one we have:

`x+2 (-x-7) = 4\\x-2x-14 = 4\\-x = 4 14\\-x = 18\\x = -18`

We find the value of y:

`y = - (- 18) -7\\y = 18-7\\y = 11`

Thus, the solution of the system is:

(-18,11)

Answer:

(-18,11)

Answer 2

Answer: (-18,11)

Explanation:

Find the x-intercept of the first equation by substituting
`y=0` and solving for "x":

`y = -x - 7\\\\x=-7`

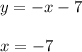
Find the y-intercept of the first equation by substituting
`x=0` and solving for "y":

`y = -x - 7\\\\y=0-7+\\\\y=-7`

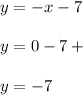
Graph the line passing through the points (-7,0) and (0,-7)

Find the x-intercept of the second equation by substituting
`y=0` and solving for "x":

`x + 2y = 4\\\\x + 2(0) = 4\\\\x=4`

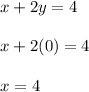
Find the y-intercept of the second equation by substituting
`x=0` and solving for "y":

`x + 2y = 4\\\\0 + 2y = 4\\\\y=2`

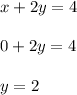
Graph the line passing through the points (4,0) and (0,2)

You can observe in the graph that the point of intersection of the lines is:

(-18,11)

This is the solution of the system of equations.