Answer:
4
Explanation:
The question is not clear. You have indicated the original function as 12sin(0) - 9sin²(0)
If so, the solution is trivial. At 0, sin(0) is 0 so the solution is 0
However, I will assume you meant the angle to be
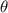 rather than 0 which makes sense and proceed accordingly
rather than 0 which makes sense and proceed accordingly
We can find the maximum or minimum of any function by finding the first derivate and setting it equal to 0
The original function is
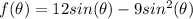
Taking the first derivative of this with respect to
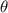 and setting it equal to 0 lets us solve for the maximum (or minimum) value
and setting it equal to 0 lets us solve for the maximum (or minimum) value
The first derivative of
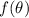 w.r.t
w.r.t
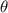 is
is
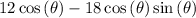
And setting this = 0 gives
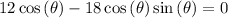
Eliminating
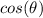 on both sides and solving for
on both sides and solving for
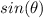 gives us
gives us
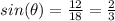
Plugging this value of
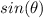 into the original equation gives us
into the original equation gives us
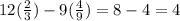
This is the maximum value that the function can acquire. The attached graph shows this as correct