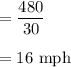Question

Riding a bike a person takes 20 minutes to go to work. The trip back home takes 30 minutes. If the rate back is 8 mph slower than the trip to work, find the rates (speeds) each way and the distance to work.

Answer 1

• Trip to work has rate: 24 mph

• Trip back to home has rate: 18 mph

• Distance to work is: 480 m

Explanation:

We know that speed is defined as the ratio of distance to time.

i.e.

`Speed=(Distance)/(Time)`

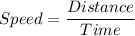
Let the distance traveled to work be: x m.

Now, while going to work it takes a person 20 minutes.

This means that the speed of the person while going to work is:

`S_1=(x)/(20)`

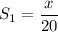
Also, the time taken to come back home is: 30 minutes.

This means that the speed of person while riding to home is:

`S_2=(x)/(30)`

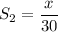
Also, it is given that the rate back is 8 mph slower than the trip to work.

This means that:

`S_1-S_2=8`

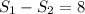
i.e.

`(x)/(20)-(x)/(30)=8\\\\i.e.\\\\(30x-20x)/(600)=8\\\\i.e.\\\\(10x)/(600)=8\\\\i.e.\\\\(x)/(60)=8\\\\i.e.\\\\x=480\ \text{m}`

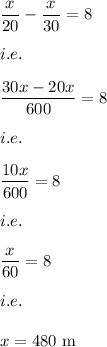
Hence, the distance to work is: 480 m.

Also, the rate while going to work is:

`=(480)/(20)\\\\=24\ \text{mph}`

and the trip back to home is covered with the speed:

`=(480)/(30)\\\\=16\ \text{mph}`