Question

Problem 4. Let m and n be two integers. Show that m^3- n^3 is even if and only if m n is even.

Answer 1

The expression
`m^3-n^3` is even if both variables (m and n) are even or both are odd

Explanation:

Let's remember the logical operations with even and odd numbers

odd*odd=odd

even*even=even

odd*even=even

odd-odd=even

even-even=even

even-odd=odd

Now, the original expression is:

`m^3-n^3` which can be expressed as:

`(m*(m*m))-(n*(n*n))`

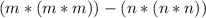
If m and n are both odd, then:

`(m*(m*m))=odd*(odd*odd)=odd*(odd)=odd`

`(n*(n*n))=odd*(odd*odd)=odd*(odd)=odd`

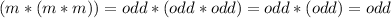
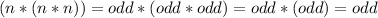
Then,
`(m*(m*m))-(n*(n*n))=odd-odd=even`

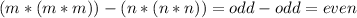
If m and n are both even, then:

`(m*(m*m))=even*(even*even)=odd*(even)=even`

`(m*(m*m))=even*(even*even)=odd*(even)=even`

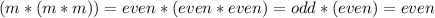
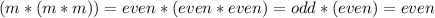
Then,
`(m*(m*m))-(n*(n*n))=even-even=even`

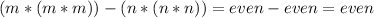
Finally if one of them is even, for example m, and the other is odd, for example n, then:

`(m*(m*m))=even*(even*even)=odd*(even)=even`

`(n*(n*n))=odd*(odd*odd)=odd*(odd)=odd`

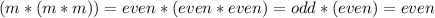
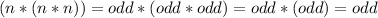
Then,
`(m*(m*m))-(n*(n*n))=even-odd=odd`

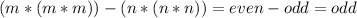
In conclusion, the expression
`m^3-n^3` is even if both variables (m and n) are even or both are odd. If one of them is even and the other one is odd, then the expression is odd.