Question

Y"+4y = 8 sin 2x. Trial Solution using annihilator technique

Linear Algebra and Differential equations
I am so confused why would you multiple by X up(x)

Answer 1

A second order linear, non - homogeneous ODE has a form of
`ay''+by'+cy=g(x)`

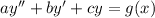
The general solution to,
`a(x)y''+b(x)y'+c(x)y=0`

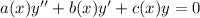
Can be written as,

`y=y_h+y_p`

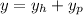
Where
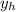`y_h` is a solution to the homogeneous ODE and
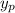`y_p` the particular solution, function that satisfies the non - homogeneous equation.

We can solve
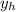`y_h` by rewriting the equation,

`ay''+by'+cy=0\Longrightarrow(e^(xy))''+4e^(xy)=0`

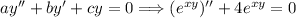
Which simplifies to,

`e^(xy)(y^2+4)=0`

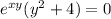
From here we get two solutions,

`y_(h1)=2i, y_(h2)=-2i`

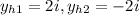
So the form here refines,

`y_h=c_1\cos(2x)+c_2\sin(2x)`

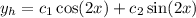
The same thing we do with
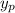`y_p` to get form of,

`y_p=-2x\cos(2x)`

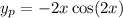
From here the final form emerges,

`y=\boxed{c_1\cos(2x)+c_2\sin(2x)-2x\cos(2x)}`

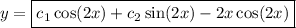
Hope this helps.

r3t40