Answer:
Solution -->
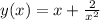
when x --> infinity the y goes to infinity too.
Explanation:
We have the eq.
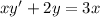
with y(1) = 3. So a reconfiguration o this last one equation can be like:
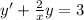
so is of the form y'+p(x) y = f(x), where the integral factor is given by:
![\mu = \exp[ \int p(x) dx]](https://img.qammunity.org/2020/formulas/mathematics/college/puh249xeu6hqhxuc0yanpd1j9m392mtgy5.png)
is,
![\mu = \exp[ \int (2)/(x) dx] = x^(2)](https://img.qammunity.org/2020/formulas/mathematics/college/lkbbus7flp8fso5qg5gjb88guwg31a55np.png)
Multiplying the whole equation with this integral factor we can write the expression:
![\int (d)/(dx)[y x^(2)] dx = \int 3x^(2) dx](https://img.qammunity.org/2020/formulas/mathematics/college/f8hrl3gk8xevqtsklcm3rfq60dhzln8h2w.png)
and from this we obtain,
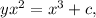
So when y(x=1) = 3, c = 2 and the complete solution can be writen as:
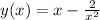 .
.
And we can see that when x --> infinity the second term of the solution is practically zero and the first is infinity so y also goes to infinity when x does.