Answer:
Point-slope form:
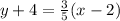
Slope-intercept form:
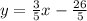
Standard form:

Explanation:
The easiest form to use here if you know it is point-slope form. I say this because you are given a point and the slope of the equation.
The point-slope form is
 .
.
Plug in your information.
Again you are given
 and
and
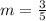 .
.
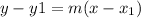 with the line before this one gives us:
with the line before this one gives us:
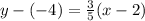
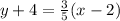 This is point-slope form.
This is point-slope form.
We can rearrange it for different form.
Another form is the slope-intercept form which is y=mx+b where m is the slope and b is the y-intercept.
So to put
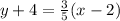 into y=mx+b we will need to distribute and isolate y.
into y=mx+b we will need to distribute and isolate y.
I will first distribute. 3/5(x-2)=3/4 x -6/5.
So now we have
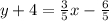
Subtract 4 on both sides:
![y=(3)/(5)x-(6)/(5)-4[tex]</p><p>Combined the like terms:</p><p>[tex]y=(3)/(5)x-(26)/(5)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/mqbaeqccwmfot8g0xjqruuqfdlh1kjng27.png) This is slope-intercept form.
This is slope-intercept form.
We can also do standard form which is ax+by=c. Usually people want a,b, and c to be integers.
So first thing I will do is get rid of the fractions by multiplying both sides by 5.
This gives me
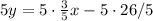
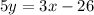
Now subtract 3x on both sides
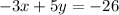
You could also multiply both sides by -1 giving you:
