Answer:
sin²θ
Explanation:
To determine what we need to divide
 by to yield
by to yield
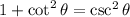 , compare equations:
, compare equations:
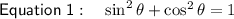
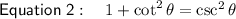
If we divide a term by itself, it will always yield 1.
Therefore, divide each term in the first equation by sin²θ:
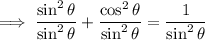
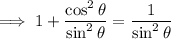

Use the trigonometric identities for cot and cosec:
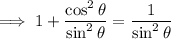
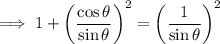
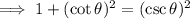
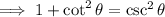
Thus proving that sin²θ + cos²θ = 1 should be divided by sin²θ to yield
1 + cot²θ = csc²θ.