Question

Seis grifos, tardan 10 horas en llenar un

depósito de 400m^3 de capacidad. ¿Cuántas
horas tardarán cuatro grifos en llenar 2
depósitos de 500m^3 cada uno?

Answer 1

6 taps....10 h......400 m³

4 taps......x h....1000 m³ (2 tanks)(500m³)

The different magnitudes are related to the magnitude of the unknown,

considering in each relationship that the magnitudes that do not intervene they remain constant in it.

So:

6 taps.....10h

4 faucets.......x h

The LESS taps, the MORE hours it will take. Inverse proportionality.

`\boldsymbol{\sf{(10)/(x)=(4)/(6) \ \ (Reverse) }}`

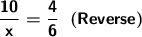
400 m³......10h

1000 m³........xh

The MORE m³, the MORE hours will be needed. Direct proportionality.

`\boldsymbol{\sf{(10)/(x)=(400)/(1000) \ \ (Direct) }}`

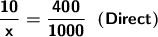
Considering that, in general, none of the magnitudes remains

1 constant, it is verified that:

`\boldsymbol{\sf{(4)/(100)=((4)/(6))((400)/(1000) ) }}`

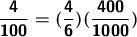
From where

`\boldsymbol{\sf{(10)/(x)=((4)(400))/((6)(1000)) }}`

`\boldsymbol{\sf{x=((10)(6)(1000))/((4)(400) )=(6000)/(1600)=\boxed{\boldsymbol{\sf{37.5}}} }}`

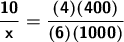
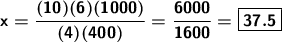
Answer: It will take 37.5 hours. That is: 37 hours and 30 minutes.✅