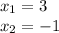For this case we must find the x-intersepts values of the following equation:
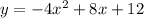
Doing y = 0 we have:
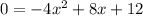
Dividing between -4 on both sides of the equation:
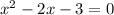
We factor, we look for two numbers that when multiplied by -3 and when added by -2. These are -3 and 1:
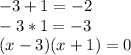
Thus, the x-intercepts values are:
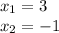
Answer: