Question

Matrices X and Y both measure 2x2 and are inverses of each other. Which matrix represents their product?

Answer 1

`\left[\begin{array}{ccc}1&0\\0&1\end{array}\right]`

Explanation:

We are asked find the matrix that represent the product of matrices X and Y both measures
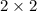`2* 2` and inverse of each other.

For a matrix multiplication to be defined, the number of columns in the first matrix must be equal to number of rows in the second matrix.

Since the both matrices are
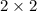`2* 2` (same number of column and row), then the product of both matrices would result in
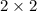`2* 2` matrices.

We also know that the multiplication of a matrix with its inverse results in identity matrix.

Therefore, our matrix would be a
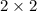`2* 2` identity matrix as:

`\left[\begin{array}{ccc}1&0\\0&1\end{array}\right]`.

Answer 2

When a matrix is multiplied by its inverse the result will be the identity matrix. If we multiply two matrix with the same size, the resulting matrix will have the same dimension.

Therefore, if we multiply the matrices X and Y we will get a 2x2 identity matrix, as follows:

`\left[\begin{array}{ccc}1&0\\0&1\\\end{array}\right]`