Answer:
The investment be worth $23328 after 11 years.
Explanation:
It is given that the annual growth reflects a geometric sequence.
An initial investment of $3 is worth $108 after 5 years.
It means the initial value of first term of the gp, a₁ = 3
The 5th term of the gp, a₅ = 108
The nth term of a gp is
 .... (1)
.... (1)
where, a is first term and r is common ratio.
The 5th term of the gp is
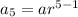
From the given information it is clear that the 5th term of the gp is 108. Substitute a₅ = 108 and a=3.

Divide both sides by 3.

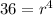
Taking fourth root on both the sides.
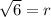
Substitute r=√6, a=3 and n=11 to find the investment worth after 11 years.
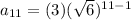
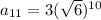
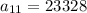
Therefore the investment worth $23328 after 11 years.