Question

The graph of f(x) = 2x is shown on the grid.

The graph of g(x) = (1/2)x is the graph of f(x) = 2x reflected over the y-axis. Which graph represents g(x)?

Answer 1

Answer with explanation:

When a graph gets reflected over y-axis it means that a horizontal reflection reflects a graph horizontally over the y-axis.

The graph of
`f(x) = 2^x` is shown on the grid.

The graph of
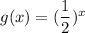`g(x) = ((1)/(2))^x` is the graph of f(x) reflected over the y-axis.

For x= 0 ,
`g(x) = ((1)/(2))^0=1`

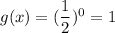
For x= 1 ,
`g(x) = ((1)/(2))^1=(1)/(2)=0.5`

For x= 2 ,
`g(x) = ((1)/(2))^2=(1)/(4)=0.25`

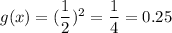
i.e. graph of g(x) passes through (-1,2) , (0,1) , (1,0.5) , (2,0.25)

From all the given graph , the correct graph is shown below .

It is showing the exact mirror-image of the given graph across y-axis and it is passing through the(-1,2) , (0,1) , (1,0.5) , (2,0.25) .

Answer 2

see below

Explanation:

Oddly enough, it is the one that with f(x) reflected over the y-axis. All points on the graph are mirrored across that axis (x is changed to -x, y is left alone).