Answer:

Step-by-step explanation:
For unbanked road the maximum friction force will provide centripetal force to the car.
So here we will have

Since we know that centripetal force here is due to friction force
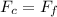
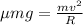
now for two cars we will have
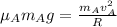
also we have
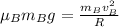
now by division of two equations
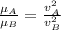
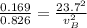
so we will have
