ANSWER
B. No real solutions
EXPLANATION
The given equation is

By comparing to
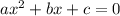
We have a=3,b=1 and c=10.
We substitute these values into the formula
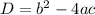
to determine the nature of the roots.

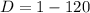
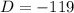
The discriminant is negative.
This means that the given quadratic equation has no real roots.