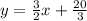Question

Draw a line perpendicular to the line that contains the points

(1, 8)
and
(4, 6)
and passes through the point
(−2, 8)

Answer 1

`y=(3)/(2) x+(20)/(3)`

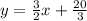
Explanation:

First, to find the original line, employ the slope formula.

`(y2-y1)/(x2-x1) \\\\(6-8)/(4-1) \\\\(-2)/(3)`

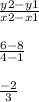
The slope of your original line is
`-(2)/(3)`.

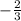Next, plug in your slope and the third point to the point-slope formula.

`y-y1=m(x-x1)\\\\y-8=-(2)/(3) (x+2)\\\\y-8=-(2)/(3) x-(4)/(3)\\\\y=-(2)/(3) x+(20)/(3)`

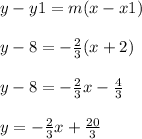
To find the line which is perpendicular to the line, take the opposite reciprocal of the slope.

To find the opposite, flip the sign.
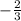`-(2)/(3)` is negative, so it will become
`(2)/(3)`, which is positive.

To find the reciprocal, flip the fraction.
`(2)/(3)` would become
`(3)/(2)`.

Your slope for the perpendicular line is
`(3)/(2)`, so your line is:

`y=(3)/(2) x+(20)/(3)`